Publications
Peer-Reviewed Research Articles
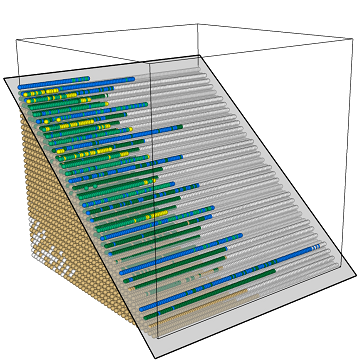
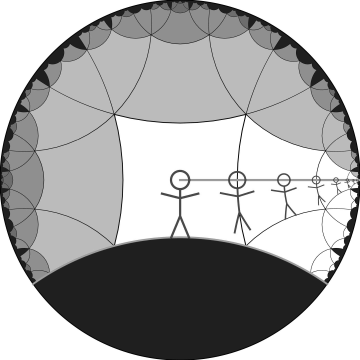
(↑ top)Holonomy: A Virtual Environment based on Hyperbolic Space
2024: Martin Skrodzki, Scott Jochems, Joris Rijsdijk, Ravi Snellenberg, Rafael Bidarra
In: Proceedings of the 29th International ACM Conference on 3D Web Technology
Holonomy is a virtual environment based on the mathematical concept of hyperbolic geometry. Unlike other environments, Holonomy allows users to seamlessly explore an infinite hyperbolic space by physically walking. They use their body as the controller, eliminating the need for teleportation or other artificial VR locomotion methods. This paper discusses the development of Holonomy, highlighting the technical challenges faced and overcome during its creation, including rendering complex hyperbolic environments, populating the space with objects, and implementing algorithms for finding shortest paths in the underlying non-Euclidean geometry. Furthermore, we present a proof-of-concept implementation in the form of a VR navigation game and some preliminary learning outcomes from this implementation.
Preprint Article in the Journal APK for Meta Quest 3 Fast Forward Video
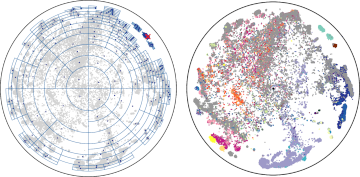
Accelerating hyperbolic t-SNE
2024: Martin Skrodzki, Hunter van Geffen, Nicolas F. Chaves-de-Plaza, Thomas Höllt, Elmar Eisemann, Klaus Hildebrandt
In: IEEE Transactions on Visualization and Computer Graphics (TVCG)
The need to understand the structure of hierarchical or high-dimensional data is present in a variety of fields. Hyperbolic spaces have proven to be an important tool for embedding computations and analysis tasks as their non-linear nature lends itself well to tree or graph data. Subsequently, they have also been used in the visualization of high-dimensional data, where they exhibit increased embedding performance. However, none of the existing dimensionality reduction methods for embedding into hyperbolic spaces scale well with the size of the input data. That is because the embeddings are computed via iterative optimization schemes and the computation cost of every iteration is quadratic in the size of the input. Furthermore, due to the non-linear nature of hyperbolic spaces, Euclidean acceleration structures cannot directly be translated to the hyperbolic setting. This paper introduces the first acceleration structure for hyperbolic embeddings, building upon a polar quadtree. We compare our approach with existing methods and demonstrate that it computes embeddings of similar quality in significantly less time.
Preprint
Article in the Journal
Implementation
 Replicability Stamp
Fast Forward Video
Replicability Stamp
Fast Forward Video
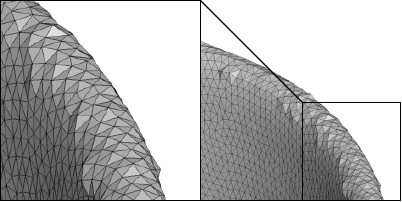
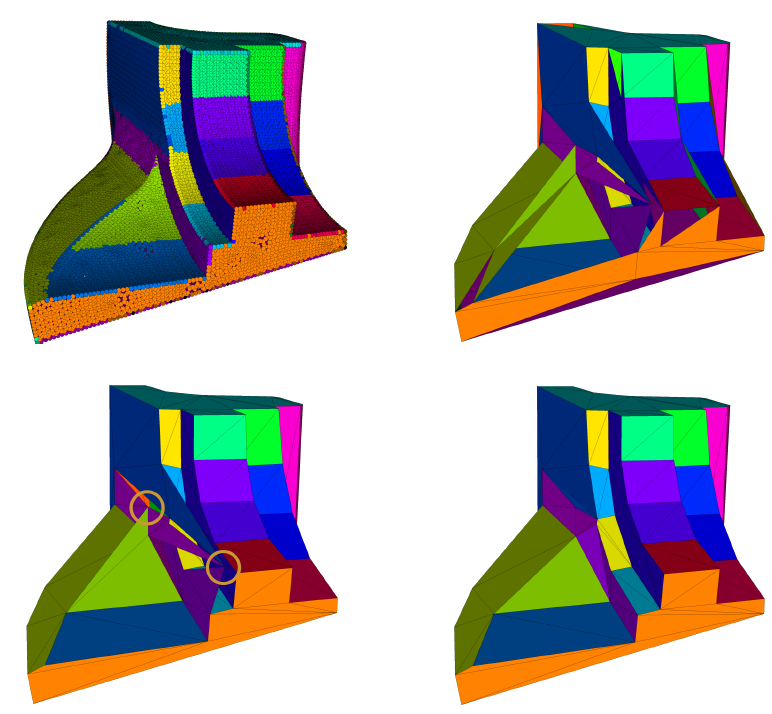
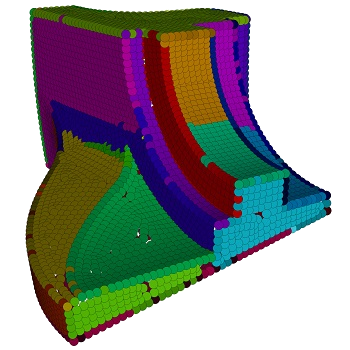
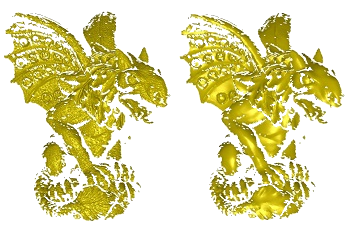
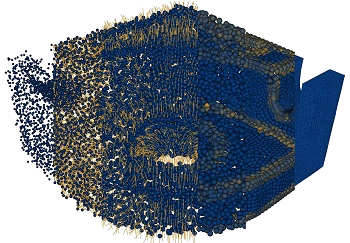
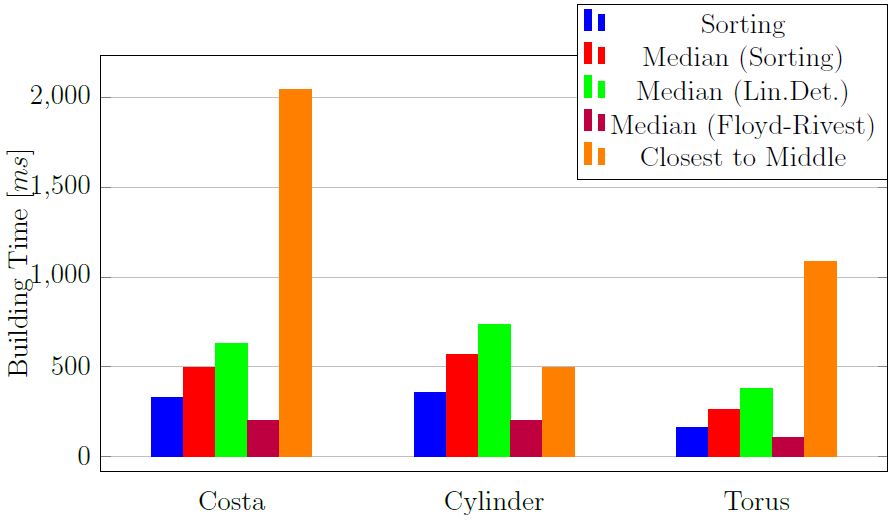
Manifold Meshing of Point Clouds with Guaranteed Smallest Edge Length
2024: Henriette Lipschütz, Ulrich Reitebuch, Konrad Polthier, and Martin Skrodzki
In: Proceedings of the 2024 International Meshing Roundtable (IMR)
Point clouds and polygonal meshes are widely used when modeling real-world scenarios. Here, point clouds arise, for instance, from acquisition processes applied in various surroundings, such as reverse engineering, rapid prototyping, or cultural preservation. Based on these raw data, polygonal meshes are created to, for example, run various simulations. For such applications, the utilized meshes must be of high quality. This paper presents an algorithm to derive triangle meshes from unstructured point clouds. The occurring edges have a close to uniform length and their lengths are bounded from below. Theoretical results guarantee the output to be manifold, provided suitable input and parameter choices. Further, the paper presents several experiments establishing that the algorithms can compete with widely used competitors in terms of quality of the output and timing. Furthermore, the output is stable under moderate levels of noise.
Preprint Bibtex Article in the Journal Extended version in the ArXiv Supplementary material and implementation details
On the importance of illustration for mathematical research
2024: Rémi Coulon, Gabriel Dorfsman-Hopkins, Edmund Harriss, Martin Skrodzki, Katherine E. Stange, Glen Whitney
In: Notices of the American Mathematical Society
Mathematical understanding is built in many ways. Among these, illustration has been a companion and tool for research for as long as research has taken place. We use the term illustration to encompass any way one might bring a mathematical idea into physical form or experience, including hand-made diagrams or models, computer visualization, 3D printing, and virtual reality, among many others. The very process of illustration itself challenges our mathematical understanding and forces us to answer questions we may not have posed otherwise. It can even make mathematics an experimental science, in which immersive exploration of data and representations drive the cycle of problem, conjecture, and proof. Today, modern technology for the first time places the production of highly complicated models within the reach of many individual mathematicians. Here, we sketch the rich history of illustration, highlight important recent examples of its contribution to research, and examine how it can be viewed as a discipline in its own right.
Preprint Bibtex Article in the Journal Extended version in the ArXiv
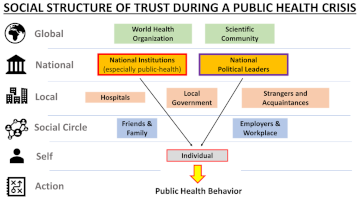
Trust in Institutions, Not in Political Leaders, Determines Compliance in COVID-19 Prevention Measures within Societies across the Globe
2022: Ryan P. Badman, Ace X. Wang, Martin Skrodzki, Heng-Chin Cho, David Aguilar-Lleyda, Naoko Shiono, Seng Bum Michael Yoo, Yen-Sheng Chiang, and Rei Akaishi
In: Behavioral Sciences
A core assumption often heard in public health discourse is that increasing trust in national political leaders is essential for securing public health compliance during crises such as the COVID-19 pandemic (2019–ongoing). However, studies of national government trust are typically too coarse-grained to differentiate between trust in institutions versus more interpersonal trust in political leaders. Here, we present multiscale trust measurements for twelve countries and territories across the West, Oceania and East Asia. These trust results were used to identify which specific domains of government and social trust were most crucial for securing public health compliance (frequency of mask wearing and social distancing) and understanding the reasons for following health measures (belief in effectiveness of public health measures). Through the use of linear regression and structural equation modeling, our cross-cultural survey-based analysis (N = 3369 subjects) revealed that higher trust in national and local public health institutions was a universally consistent predictor of public health compliance, while trust in national political leaders was not predictive of compliance across cultures and geographical regions. Institutional trust was mediated by multiple types of transparency, including providing rationale, securing public feedback, and honestly expressing uncertainty. These results highlight the importance of distinguishing between components of government trust, to better understand which entities the public gives the most attention to during crises.
Surface Denoising based on Normal Filtering in a Robust Statistics Framework
2021: Sunil Kumar Yadav, Martin Skrodzki, Eric Zimmermann, and Konrad Polthier
In: Mathematics for Industry book series (MFI), volume 35
During a surface acquisition process using 3D scanners, noise is inevitable and an important step in geometry processing is to remove these noise components from these surfaces (given as points-set or triangulated mesh). The noise-removal process (denoising) can be performed by filtering the surface normals first and by adjusting the vertex positions according to filtered normals afterwards. Therefore, in many available denoising algorithms, the computation of noise-free normals is a key factor. A variety of filters have been introduced for noise-removal from normals, with different focus points like robustness against outliers or large amplitude of noise. Although these filters are performing well in different aspects, a unified framework is missing to establish the relation between them and to provide a theoretical analysis beyond the performance of each method.
In this paper, we introduce such a framework to establish relations between a number of widely-used nonlinear filters for face normals in mesh denoising and vertex normals in point set denoising. We cover robust statistical estimation with M-smoothers and their application to linear and non-linear normal filtering. Although these methods originate in different mathematical theories - which include diffusion-, bilateral-, and directional curvature-based algorithms - we demonstrate that all of them can be cast into a unified framework of robust statistics using robust error norms and their corresponding influence functions. This unification contributes to a better understanding of the individual methods and their relations with each other. Furthermore, the presented framework provides a platform for new techniques to combine the advantages of known filters and to compare them with available methods.
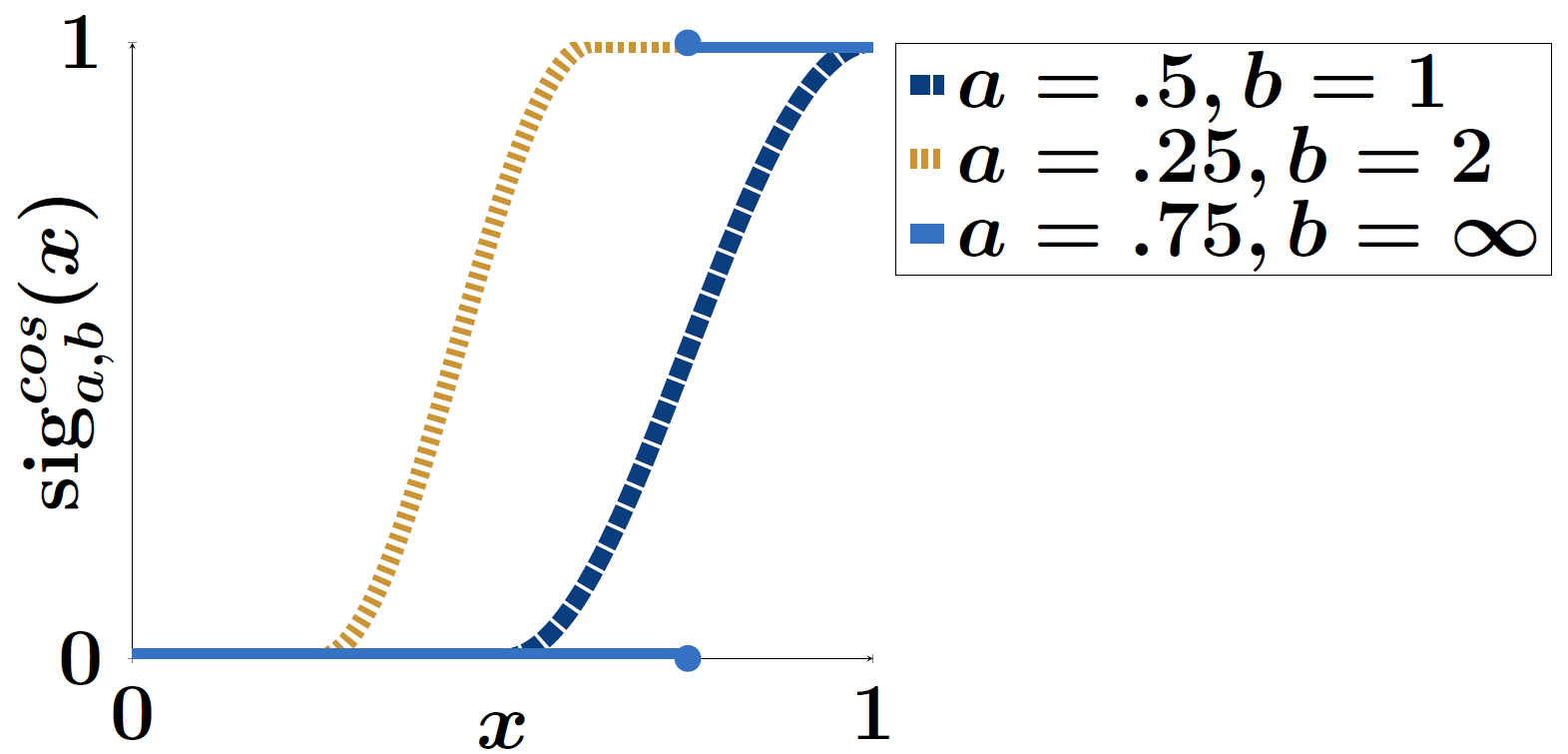
A Large-Scale Evaluation Of Shape-Aware Neighborhood Weights And Neighborhood Sizes
2021: Martin Skrodzki and Eric Zimmermann
In: Computer-Aided Design, Vol. 141
In this paper, we define and evaluate a weighting scheme for neighborhoods in point sets. Our weighting takes the shape of the geometry, i.e., the normal information, into account. This causes the obtained neighborhoods to be more reliable in the sense that connectivity also depends on the orientation of the point set. We utilize a sigmoid to define the weights based on the normal variation. For an evaluation of the weighting scheme, we turn to a Shannon entropy model for feature classification that can be proven to be non-degenerate for our family of weights. Based on this model, we evaluate our weighting terms on a large scale of both clean and real-world models. This evaluation provides results regarding the choice of optimal parameters within our weighting scheme. Furthermore, the large-scale evaluation also reveals that neighborhood sizes should not be fixed globally when processing models. Finally, we highlight the applicability of our weighting scheme within the application context of denoising.
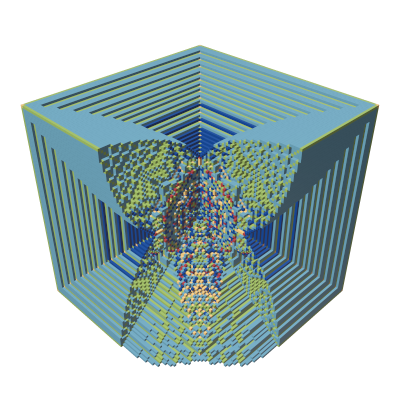
Experimental visually-guided investigation of sub-structures in three-dimensional Turing-like patterns
2021: Martin Skrodzki, Ulrich Reitebuch, and Eric Zimmermann
In: Exploratory Papers of Automata 2021
In this paper, we are interested in classifying the different arising (topological) structures of three-dimensional Turing-like patterns. By providing examples for the different structures, we confirm a conjecture regarding these structures within the setup of three-dimensional Turing-like pattern. Furthermore, we investigate how these structures are distributed in the parameter space of the discrete model. We found twofold versions of so-called "zero-" and "one-dimensional" structures as well as "two-dimensional" structures and use our experimental findings to formulate several conjectures for three-dimensional Turing-like patterns and higher-dimensional cases.
Preprint Bibtex Article in HAL Extended version in the ArXiv Talk on YouTube
Single-sized spheres on surfaces (S4)
2021: Henriette Lipschütz, Martin Skrodzki, Ulrich Reitebuch, and Konrad Polthier
In: Computer Aided Geometric Design, Vol. 85
Surface representations play a major role in a variety of applications throughout a diverse collection of fields, such as biology, chemistry, physics, or architecture. From a simulation point of view, it is important to simulate the surface as good as possible, including the usage of a wide range of different approximating elements. However, when it comes to manufacturing, it is desirable to have as few different building blocks as possible, as these can then be produced cost-efficiently.
Our paper adds a procedure to be used in the simulation of natural phenomena as well as within the designers' creative toolbox. It represents a surface via a collection of equally sized spheres. In the first part of the paper, we give a mathematically precise definition of the underlying problem: How to cover as much as possible of a surface by single-sized spheres. This leads to questions regarding the extremal intersection area of spheres with reasonably well-behaved surfaces, for which we present upper and lower bounds. From these, we deduce how many spheres of a certain, fixed radius can be used at least and at most when interpolating a surface.
Following these theoretical results, we compare a depth-first, a breadth-first, and a heuristic algorithm for the generation of surface coverings by single-sized spheres. As opposed to the mathematical description, we show that our algorithms also work for surfaces with boundary elements or sharp features such as edges or corners. We prove the applicability of our algorithm by a multitude of experiments and compare our procedure to ellipsoidal and multi-sized sphere methods.
Variational Shape Approximation of Point Set Surfaces
2020: Martin Skrodzki, Eric Zimmermann, and Konrad Polthier
In: Computer Aided Geometric Design, Vol. 80
In this work, we present a translation of the complete pipeline for variational shape approximation (VSA) to the setting of point sets. First, we describe an explicit example for the theoretically known non-convergence of the currently available VSA approaches. The example motivates us to introduce an alternate version of VSA based on a switch operation for which we prove convergence. Second, we discuss how two operations – split and merge – can be included in a fully automatic pipeline that is in turn independent of the placement and number of initial seeds. Third and finally, we present two approaches how to obtain a simplified mesh from the output of the VSA procedure. This simplification is either based on simple plane intersection or based on a variational optimization problem. Several qualitative and quantitative results prove the relevance of our approach.
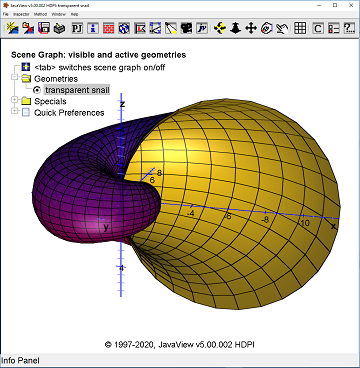
How the Deprecation of Java Applets Affected Online Visualization Frameworks – A Case Study
2020: Martin Skrodzki
In: VisGap - The Gap between Visualization Research and Visualization Software
The JavaView visualization framework was designed at the end of the 1990s as a software that provides-among other services- easy, interactive geometry visualizations on web pages.We discuss how this and other design goals were met and present several applications to highlight the contemporary use-cases of the framework. However, as JavaView's easy web exports was based on Java Applets, the deprecation of this technology disabled one main functionality of the software. The remainder of the article uses JavaView as an example to highlight the effects of changes in the underlying programming language on a visualization toolkit. We discuss possible reactions of software to such challenges, where the JavaView framework serves as an example to illustrate development decisions. These discussions are guided by the broader, underlying question as to how long it is sensible to maintain a software.
Preprint Bibtex Entry in the EG Digital Library Talk on YouTube
Large-scale Evaluation of Neighborhood Weights and Sizes
2020: Martin Skrodzki and Eric Zimmermann
In: SPM/SMI 2020 Conference Poster Proceedings
We evaluate a weighting scheme for neighborhoods in point sets, which takes the normal information of the points into account. We utilize a sigmoid to define the weights based on the normal variation. For an evaluation, we turn to a Shannon entropy model for feature separation and evaluate our weight terms on a large scale of models.
Variational Shape Approximation of Point Set Surfaces
2019: Martin Skrodzki, Eric Zimmermann, and Konrad Polthier
In: International Geometry Summit 2019 – Poster Proceedings
This work proposes an algorithm for point set segmentation based on the concept of Variational Shape Approximation (VSA), which uses the k-means approach. It iteratively selects seeds, grows flat planar proxy regions according to normal similarity, and updates the proxies. It is known that this algorithm does not converge in general. We provide a concrete example showing that the utilized error measure can indeed grow during the run of the algorithm. To reach convergence, we propose a modification of the original VSA. Further, we provide two new operations applied to the proxy regions, namely split and merge, which enqueue in the pipeline and act according to a user-given parameter. The advantages over regular VSA are independence of both a prescribed number of proxies and a (manual) selection of seeds. Especially the latter is a common drawback of region-growing approaches in segmentation.
Constraint-based point set denoising using normal voting tensor and restricted quadratic error metrics
2018: Sunil Kumar Yadav, Ulrich Reitebuch, Martin Skrodzki, Eric Zimmermann, and Konrad Polthier
In: Computers & Graphics, Volume 74
In many applications, point set surfaces are acquired by 3D scanners. During this acquisition process, noise and outliers are inevitable. For a high fidelity surface reconstruction from a noisy point set, a feature preserving point set denoising operation has to be performed to remove noise and outliers from the input point set. To suppress these undesired components while preserving features, we introduce an anisotropic point set denoising algorithm in the normal voting tensor framework. The proposed method consists of three different stages that are iteratively applied to the input: in the first stage, noisy vertex normals, are initially computed using principal component analysis, are processed using a vertex-based normal voting tensor and binary eigenvalues optimization. In the second stage, feature points are categorized into corners, edges, and surface patches using a weighted covariance matrix, which is computed based on the processed vertex normals. In the last stage, vertex positions are updated according to the processed vertex normals using restricted quadratic error metrics. For the vertex updates, we add different constraints to the quadratic error metric based on feature (edges and corners) and non-feature (planar) vertices. Finally, we show our method to be robust and comparable to state-of-the-art methods in several experiments.
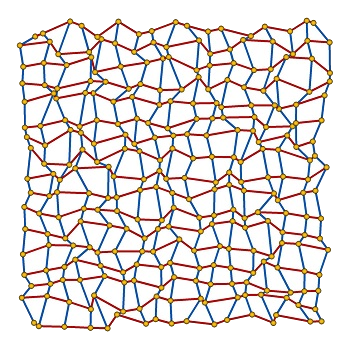
Combinatorial and Asymptotical Results on the Neighborhood Grid Data Structure
2018: Martin Skrodzki, Ulrich Reitebuch, Konrad Polthier, and Shagnik Das
In: EuroCG 2018 Extended Abstracts
In 2009, Joselli et al. introduced the Neighborhood Grid data structure for fast computation of neighborhood estimates in point sets. Even though the data structure has been used in several applications and shown to be practically relevant, it is theoretically not yet well understood. The purpose of this paper is to give results on the complexity of building algorithms – both singlecore and parallel – for the neighborhood grid. Furthermore, current investigations on related combinatorial questions are presented.
Directional Density Measure To Intrinsically Estimate And Counteract Non-Uniformity In Point Clouds
2018: Martin Skrodzki, Johanna Jansen, and Konrad Polthier
In: Computer Aided Geometric Design, Volume 64
With the emergence of affordable 3D scanning and printing devices, processing of large point clouds has to be performed in many applications. Several algorithms are available for surface reconstruction, smoothing, and parametrization. However, many of these require the sampling of the point cloud to be uniform or at least to be within certain controlled parameters. For nonuniformly sampled point clouds, some methods have been proposed that deal with the nonuniformity by adding additional information such as topological or hierarchical data. In this paper, we focus on point clouds sampling surfaces in R3. We present the notion of local directional density measure that can be intrinsically computed within the point cloud, that is without further knowledge of the geometry despite the given point samples. Specifically, we build on previous work to derive a local, directed, and discrete measure for density. Furthermore, we derive another discrete and a smooth density measure and compare these three experimentally. Each of the three considered measures gives density weights to use in discretizations of operators such that these become independent of sampling uniformity. We demonstrate the effectiveness of our method on both synthetic and real world data.
Peer-Reviewed Visualization, Illustration, and Education Articles
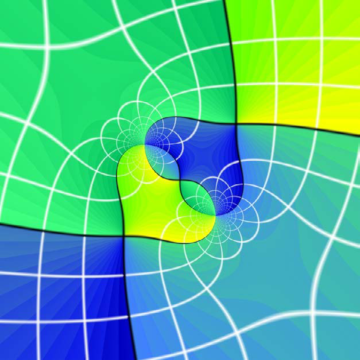
(↑ top)Heart of Domain Coloring
2024: Ulrich Reitebuch, Henriette Lipschütz, Konrad Polthier, Martin Skrodzki.
In: Proceedings of Bridges 2024: Mathematics, Art, Music, Architecture, Culture
Domain coloring allows for visualization of complex functions. In this paper, we give a brief introduction to domain coloring in general. Then, we investigate its capabilities to create specific shapes, namely hearts. Finally, we present a gallery of our findings.
Whirling Tiles
2023: Ulrich Reitebuch, Martin Skrodzki, Henriette Lipschütz, Konrad Polthier.
In: Proceedings of Bridges 2023: Mathematics, Art, Music, Architecture, Culture
Whirling kites, a pattern occurring in Islamic geometric ornaments, is the main inspiration for this paper. First, the pattern is presented as well as different perspectives on how to create it. Then, one of these perspectives is generalized in order to obtain a family of patterns. Finally, we apply the generalization to show these patterns on several tilings.
Graph Theory and Arts: A Course Retrospective
2023: Henriette Lipschütz, Martin Skrodzki.
In: Proceedings of Bridges 2023: Mathematics, Art, Music, Architecture, Culture
During a course conducted in 2022, the participants investigated connections between mathematics and art. Based on a brief introduction to graph theory and inspired by some existing mathematical artworks, the participants—in this case, high school students—created representations on their own. This paper discusses underlying motivations, the course concept, an approach to idea generation, and the resulting artworks created by the course participants.
Science Communication and Outreach Events During the Illustrating Mathematics Semester Program at the Institute for Computational and Experimental Research in Mathematics (ICERM)
2023: Martin Skrodzki.
In: Anna Maria Hartkopf and Erin Henning (eds.), Handbook of Mathematical Science Communication
Good illustrations of mathematical content enhance the science communication of mathematics as
well as the scientific process itself. However, the creation of these illustrations, the rendering of
videos, the process of mathematical making1, is still underdeveloped and undervalued by many
professional mathematicians2. The semester program Illustrating Mathematics aimed at closing some
of the gaps between the richness of mathematical content and the availability of corresponding
illustrations by creating new and novel ways to show and present mathematics.
This article reports on the program's related science communication and public outreach activities.
To present the frame in which the activities took place, the first two sections briefly introduce the
institutional setup and the scientific aspects of the semester program. The following sections each
present one outreach activity in detail.
Mathematik und Kunst im Rahmen der Deutschen SchülerAkademie
2022: Henriette Lipschütz und Martin Skrodzki.
In: Mitteilungen der Deutschen Mathematiker-Vereinigung
Bereits die ersten überlieferten mathematischen Texte sind reich illustriert. Der direkte Zusammenhang von Mathematik und Kunst ist spätestens seit der Verwendung der Zentralperspektive in der Renaissance evident. Dieser Artikel stellt ein Kurskonzept vor, das das Zusammenspiel von Mathematik und Kunst als eigenen Zugang nutzt, um das Verständnis mathematischer Inhalte zu vertiefen. Ein besonderes Augenmerk soll den Werken gelten, die durch die Teilnehmenden bei zwei Erprobungen des Kurskonzeptes im Rahmen der Deutschen SchülerAkademie erstellt wurden.
Wooden Mathematics – Making abstraction tangible
2022: Milena Damrau, Martin Skrodzki, Nicholas Bruscia, Aaron Fenyes, Teresa Hunyadi, and Dave Murray-Rust.
In: Between Science & Art
Wooden artworks can be found throughout all art historical periods. Yet, they are scarcely found in the realm of mathematical art. The introductory article of this collection briefly presents the contributors and the structure of their contributions. In the following, each article exemplifies the interaction of wood as both an artistic medium and a means for the illustration of mathematical content.
Linked Knots from the Gyro Operation on the Dodecahedron
2022: Henriette Lipschütz, Martin Skrodzki, Ulrich Reitebuch, and Konrad Polthier
In: Proceedings of Bridges 2022: Mathematics, Art, Music, Architecture, Culture
John Horton Conway's taxonomy for Archimedean and Catalan solids includes the snub and the dual operation, their combination being known as the gyro operation. Intriguingly, recent work showed that the gyro operation can be used to create weaving patterns when applied to planar n-gons. This process can be applied to two-dimensional polyhedral surfaces in ℝ³. In this paper, we investigate the weaving structures that are created on the dodecahedron. We show that the weaving structures can be interpreted via knot theory and written in form of a link diagram. Furthermore, we prove the number of knots arising on the dodecahedron to be six. Finally, we present hand-crafted physical representations of the results in form of balls made of yarn, inspired by Japanese temari.
Chip-Firing Revisited: A Peek into the Third Dimension
2022: Martin Skrodzki and Ulrich Reitebuch
In: Proceedings of Bridges 2022: Mathematics, Art, Music, Architecture, Culture
Chip-firing was first introduced as a probabilistic game. Subsequently, it was generalized to arbitrary graph configurations and investigated mostly with regard to two-dimensional quad-grid layouts. In this paper, we lift chip-firing to the third dimension. Aside from the arising three-dimensional shapes, we are interested in the internal, two-dimensional structures. Furthermore, we explore the different shapes obtained by chip firing processes on various neighborhoods, such as the face-centered and the cube-centered grid as well as on a neighborhood inspired by knight moves.
Weaving patterns inspired by the pentagon snub subdivision scheme
2022: Henriette Lipschütz, Ulrich Reitebuch, Martin Skrodzki, Konrad Polthier
In: Journal of Mathematics and the Arts
Various computer simulations regarding, e.g. the weather or structural mechanics, solve complex problems on a two-dimensional domain. They mostly do so by splitting the input domain into a finite set of smaller and simpler elements on which the simulation can be run fast and efficiently. This process of splitting can be automatized by using subdivision schemes. Given the wide range of simulation problems to be tackled, an equally wide range of subdivision schemes is available. This paper illustrates a subdivision scheme that splits the input domain into pentagons. Repeated application gives rise to fractal-like structures. Furthermore, the resulting subdivided domain admits to certain weaving patterns. These patterns are subsequently generalized to several other subdivision schemes. As a final contribution, we provide paper models illustrating the weaving patterns induced by the pentagonal subdivision scheme. Furthermore, we present a jigsaw puzzle illustrating both the subdivision process and the induced weaving pattern. These transform the visual and abstract mathematical algorithms into tactile objects that offer exploration possibilities aside from the visual.
Benefits of Online Meetings for the MathArt Community: Experiences from Two Events
2022: Martin Skrodzki and Milena Damrau
In: Journal of Mathematics and the Arts
Recent years saw a rapid increase in conference formats that take place either fully online or in a hybrid fashion with some people on-site and others online. While these formats brought new challenges, they also opened up new opportunities. In the present article, we first outline advantages and disadvantages of different conference formats as discussed in the literature. We then share our own experiences based on two mathematics and art events that occurred during the respective annual meetings of the German Mathematical Society in 2020 and 2021. This is to illustrate the main benefits of online formats, in particular for the MathArt community. We conclude by highlighting two specific aspects – the facilitated presentation of large artworks and the availability of talk recordings – and give a brief outlook on hybrid events.
Illustrations of non-Euclidean geometry in virtual reality
2021: Martin Skrodzki
In: Lars C. Grabbe, Patrick Rupert-Kruse, Norbert M. Schmitz (Editors), Virtual Images: Trilogy of Synthetic Realities I
Mathematical objects are generally abstract and not very approachable. Illustrations and interactive visualizations help both students and professionals to comprehend mathematical material and to work with it. This approach lends itself particularly well to geometrical objects. An example for this category of mathematical objects are hyperbolic geometric spaces. When Euclid lay down the foundations of mathematics, his formulation of geometry reflected the surrounding space, as humans perceive it. For about two millennia, it remained unclear whether there are alternative geometric spaces that carry their own, unique mathematical properties and that do not reflect human every-day perceptions. Finally, in the early 19th century, several mathematicians described such geometries, which do not follow Euclid's rules and which were at first interesting solely from a pure mathematical point of view. These descriptions were not very accessible as mathematicians approached the geometries via complicated collections of formulae. Within the following decades, visualization aided the new concepts and two-dimensional versions of these illustrations even appeared in artistic works. Furthermore, certain aspects of Einstein's theory of relativity provided applications for non-Euclidean geometric spaces. With the rise of computer graphics towards the end of the twentieth century, three-dimensional illustrations became available to explore these geometries and their non-intuitive properties. However, just as the canvas confines the two-dimensional depictions, the computer monitor confines these three-dimensional visualizations. Only virtual reality recently made it possible to present immersive experiences of non-Euclidean geometries. In virtual reality, users have completely new opportunities to encounter geometric properties and effects that are not present in their surrounding Euclidean world.
Approximating Logarithmic Spirals by Quarter Circles
2021: Ulrich Reitebuch, Martin Skrodzki, and Konrad Polthier
In: Proceedings of Bridges 2021: Mathematics, Music, Art, Architecture, Education, Culture.
The approximation of a golden logarithmic spiral by quarter circles is well known. Starting from this, we show that any logarithmic spiral can be approximated by quarter circles in a similar way. Using our construction on a rectangle with aspect ratio √𝜙 and performing a coordinate reparametrization, we obtain an aesthetic partition of the plane as our main artwork.
Preprint Bibtex Entry in the Bridges Archive Talk on YouTube
Combining Mathematics and Arts
2021: Milena Damrau, Martin Skrodzki, Anna M. Hartkopf, René M. Broeders, Katharina Hahn, David Honda, Joshua Holden, and Loe Feijs
In: Between Science & Art
The 2020 annual meeting of the German Mathematical Society saw the first minisymposium on Mathematics and Arts. The introductory article presents a classification scheme for interaction between these two disciplines. In the collection, each article exemplifies the different cases of the scheme via a contribution presented at the minisymposium.
Preprint Bibtex Paper in the online journal YouTube Playlist
Erstes Minisymposium „Mathematics and Arts” der DMV Jahrestagung 2020
2021: Milena Damrau and Martin Skrodzki
In: Mitteilungen der Deutschen Mathematiker-Vereinigung
Auf der DMV Jahrestagung 2020 fand das erste Minisymposium im Schnittbereich Mathematik und Kunst statt. Dieser Artikel fasst die Motivation, die Organisation und die Ergebnisse des Formats zusammen.
Velimir Khlebnikov's Laws of Time
2020: Martin Skrodzki, Ulrich Reitebuch, Henriette Lipschütz, and Konrad Polthier
In: Proceedings of Bridges 2020: Mathematics, Music, Art, Architecture, Education, Culture.
In February 2019, the video artist Kristina Paustian honored the Russian futurist Velimir Khlebnikov with her solo exhibition Laws of Time. The future calculations by Velimir Khlebnikov in Berlin, Germany. Among other aspects, she focused on his poetry and the mathematics used in his works. In this paper, we rephrase Khlebnikov’s ideas and thoughts in mathematical terms. Furthermore, we prove that his method of foretelling the future by analyzing several events which took place in the past produces only random results. Finally, we describe the corresponding mathematical part of the exhibition and provide an artistic exploration of Khlebnikov’s methodology.
Preprint Bibtex Entry in the Bridges Archive Talk on YouTube
Vector Fields and Paul Klee – A Summer School Course for Gifted High-School Students
2020: Martin Skrodzki and Henriette Lipschütz
In: Proceedings of Bridges 2020: Mathematics, Music, Art, Architecture, Education, Culture.
The artist Paul Klee describes and analyzes his use of symbols and colors in his book “Pädagogisches Skizzenbuch” (pedagogical sketchbook, 1925). He uses arrows for means of illustrations and also discusses the arrow itself as an element of his repertoire of symbols. Interestingly, his point of view on arrows matches the way in which vector fields are represented graphically. Based on this connection of mathematics and Klee’s artwork, we developed a concept for a summer school course for gifted high-school students. Its aim was to both introduce the participants to higher-level mathematics and to let them create their own piece of artwork related to the art of Paul Klee and vector fields. This article elaborates on the connection between Klee’s art and mathematics. It furthermore presents details of the summer course and an evaluation of its goals, including resulting artwork from participating students. Image Credit: Birgit Zickler.
Preprint Bibtex Entry in the Bridges Archive Talk on YouTube
AI and Arts – A Workshop to Unify Arts and Science
2019: Martin Skrodzki
In: w/k - Zwischen Wissenschaft & Kunst
Throughout the last years, new methods in artificial intelligence have revolutionized several scientific fields. These developments affect arts twofold. On the one hand, artists discover machine learning as a new tool. On the other hand, researchers apply the new techniques to the creative work of artists to better analyze and understand it. The workshop AI and Arts brings these two perspectives together and starts a dialog between artists and researchers. It was a satellite workshop of the KI 2019 conference in September 2019 in Kassel, Germany. The conference is the 42nd edition of the German Conference on artificial intelligence organized in cooperation with the AI Chapter of the German Society for Computer Science (GI-FBKI).
A Leap Forward: A User Study on Gestural Geometry Exploration
2019: Martin Skrodzki, Ulrike Bath, Kevin Guo, and Konrad Polthier
In: Journal of Mathematics and the Arts
Teaching mathematics in high school and university context often proves hard for both teachers and professors respectively. However, it can be supported by technology. Appliances for 3D digital setups are widely available. They have transcended their intended use as simple in- or output devices and nowadays also play a part in many artistic setups. Thus, they change the way we both perceive and create (digital) models. These changes have to be kept in mind when creating, working with, and presenting 3D art in a digital context.
In this paper, we examine the use of gesture-based controllers in the exploration of mathematical content. A user study was conducted as part of the scientific art and education exhibition “Long Night of Science”. To validate the results, a control group was presented with the same questionnaire and physical models of the mathematical objects (instead of the controller) were used. The participants of the study rated the controllers or the physical models respectively by their individually felt intuitiveness and influence on the perception of the underlying mathematical content. From the data obtained, a connection between the intuitiveness of the controller and a positive influence on the perception of the presented mathematics is shown.
Von Paradoxien, Unvollständigkeiten und Computerbeweisen: Staunen in der Mathematik
2019: Martin Skrodzki
In: Timo Kehren, Carolin Krahn, Georg Oswald, and Christoph Poetsch (Editors), Staunen. Perspektiven eines Phänomens zwischen Natur und Kultur, Fink.
Aus den einleitenden Reflexionen: „Martin Skrodzki untersucht in seinem Beitrag die Ambivalenz des Staunens, wie es sich im Umgang mit mathematischen Problemlösungen zeigt und sich so als Triebfeder wie Hemmnis in der Geschichte mathematischer Forschung auffinden lässt, wobei er die Reduktion und Eliminierung des Staunens als Grundmotiv dieser Forschung ausmacht.“
Discrete Gyroid Surface
2019: Ulrich Reitebuch, Martin Skrodzki, and Konrad Polthier
In: Proceedings of Bridges 2019: Mathematics, Music, Art, Architecture, Education, Culture.
We present a discrete gyroid surface. The gyroid is a triply periodic minimal surface, our discrete version has the same symmetries as the smooth gyroid and can be constructed from simple translational units.
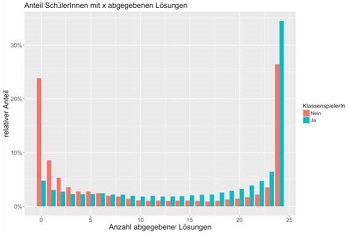
Eine Datenanalyse der Persistenz und Leistung von Schulkindern im Wettbewerb „Mathe im Advent“
2018: Milena Damrau, Hernán Villamizar, and Martin Skrodzki
In: Beiträge zum Mathematikunterricht 2018
„Mathe im Advent“ ist ein Wettbewerb, der 2008 von der Deutschen Mmathematiker-Vereinigung initiiert wurde. Jedes Jahr im Dezember öffnen Schüler*innen 24 virtuelle Türchen, hinter denen sich mathematische Probleme verstecken – verpackt in kurzen Geschichten über Wichtel. Zu jeder Frage gibt es vier Antworten, von denen genau eine richtig ist. Die Teilnehmer*innen werden dazu aufgefordert, die Aufgaben mit ihren Mitschüler*innen zu besprechen und haben einen Tag Zeit, ihre Lösungen abzugeben. Hochwertige Preise sollen zu guter Leistung motivieren. Auf Grundlage der Daten von mehr als 100.000 Schüler*innen, die 2016 am Wettbewerb teilgenommen haben, untersuchen wir den Einfluss verschiedener Faktoren auf die Leistung und auf die Wahrscheinlichkeit, dass die Schüler*innen möglichst lange am Wettbewerb teilnehmen. Dabei berücksichtigen wir Kriterien auf Basis von Einzel- und Gruppenspiel sowie den Schultyp und bestimmen durch eine Regressionsanalyse und Ereignisszeitanalyse die wichtigsten Aspekte, die zur Leistung und Persistenz beitragen.
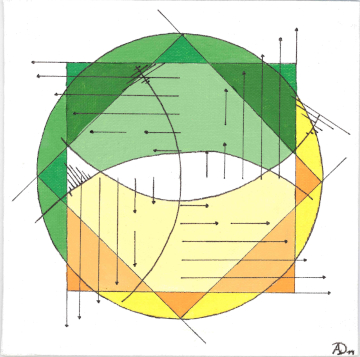
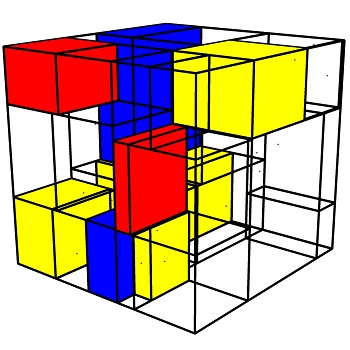
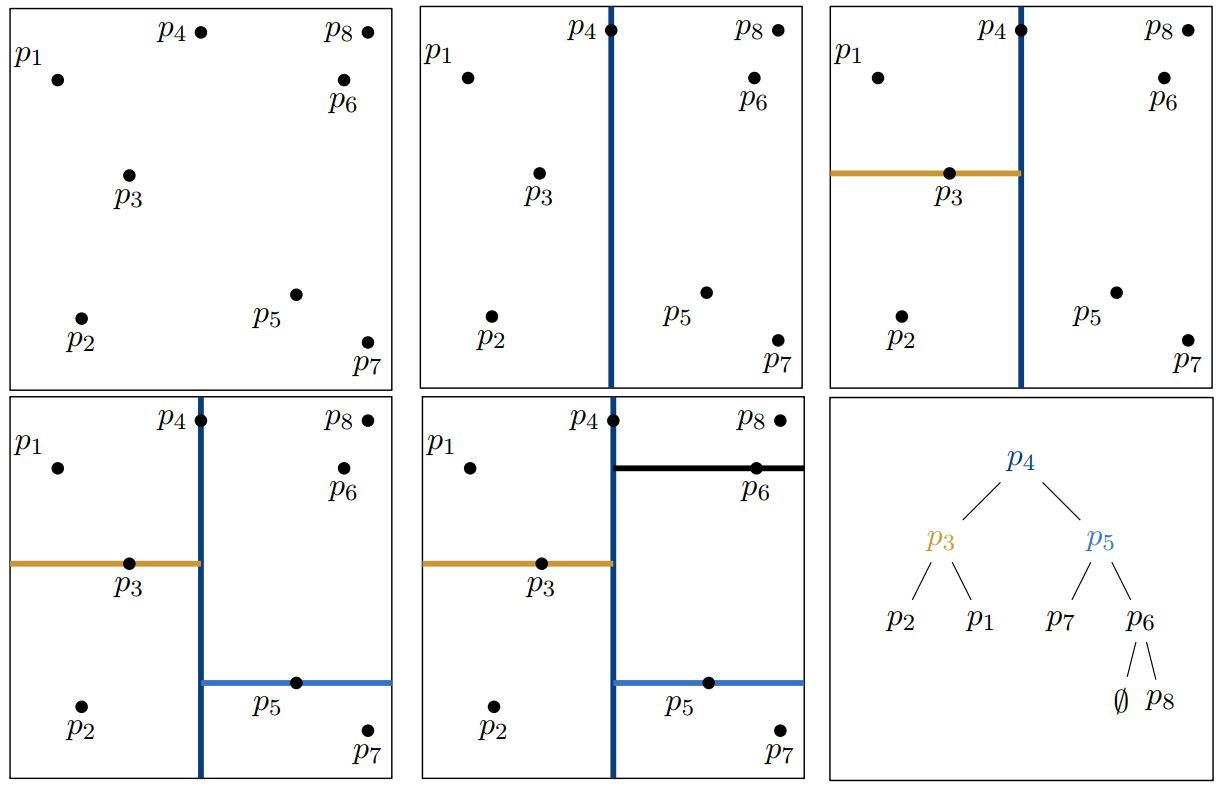
Mondrian Revisited: A Peek Into The Third Dimension
2018: Martin Skrodzki and Konrad Polthier
In: Proceedings of Bridges 2018: Mathematics, Music, Art, Architecture, Education, Culture.
The artist Piet Mondrian (1872 – 1944) is most famous for his abstract works utilizing primary colors and axes-parallel black lines. A similar structure can be found in visualizations of the KdTree data structure used in computational geometry for range searches and neighborhood queries. In this paper, we systematically explore these visualizations and their connections to Mondrian’s work and give a dimension-independent generalization of Mondrian-like pieces.
Turing Patterns Revisited: A Peek Into The Third Dimension
2017: Martin Skrodzki and Konrad Polthier
In: Proceedings of Bridges 2017: Mathematics, Music, Art, Architecture, Education, Culture.
Beginning with their introduction in 1952 by Alan Turing, Turing-like patterns have inspired research in several different fields. One of these is the field of cellular automata, which have been utilized to create Turing-like patterns by David A. Young and others. In this paper we provide a generalization of these patterns to the third dimension. Several visualizations are given to illustrate the created models.
Chladni Figures Revisited: A Peek Into The Third Dimension
2016: Martin Skrodzki, Ulrich Reitebuch and Konrad Polthier
In: Proceedings of Bridges 2016: Mathematics, Music, Art, Architecture, Education, Culture.
In his 1802 book “Acoustics”, Ernst Florens Friedrich Chladni describes how to visualize different vibration modes using sand, a metal plate, and a violin bow. We review the underlying physical and mathematical formulations and lift them to the third dimension. Finally, we present some of the resulting three dimensional Chladni figures.
Preprint Bibtex Implementation Interactive Version Entry in the Bridges Archive
ArXiv and other Preprints
(↑ top)Combinatorial and Asymptotical Results on the Neighborhood Grid
2019: Martin Skrodzki, Ulrich Reitebuch, and Alex McDonough
In 2009, Joselli et al introduced the Neighborhood Grid data structure for fast computation of neighborhood estimates in point clouds. Even though the data structure has been used in several applications and shown to be practically relevant, it is theoretically not yet well understood. The purpose of this paper is to present a polynomial-time algorithm to build the data structure. Furthermore, it is investigated whether the presented algorithm is optimal. This investigation leads to several combinatorial questions for which partial results are given. Finally, we present several limits and experiments regarding the quality of the obtained neighborhood relation.
The k-d tree data structure and a proof for neighborhood computation in expected logarithmic time
2019: Martin Skrodzki
For practical applications, any neighborhood concept imposed on a finite point set P is not of any use if it cannot be computed efficiently. Thus, in this paper, we give an introduction to the data structure of k-d trees, first presented by Friedman, Bentley, and Finkel in 1977. After a short introduction to the data structure (Section 1), we turn to the proof of efficiency by Friedman and his colleagues (Section 2). The main contribution of this paper is the translation of the proof of Freedman, Bentley, and Finkel into modern terms and the elaboration of the proof.
Theses
(↑ top)Neighborhood Data Structures, Manifold Properties, and Processing of Point Set Surfaces
2019: Martin Skrodzki
PhD Thesis
The thesis covers three topics all centered in the context of point set processing. The first topic concerns notions of neighborhood and corresponding data structures. The second main topic of this thesis deals with manifold structures for point set surfaces. Third and finally, algorithms have to work efficiently and robustly on the point set. While meshed geometries provide an intuitive and natural weighting by the areas of the faces, point sets can at most work with distances between the points. This introduces a new level of difficulty to be overcome by any point set processing algorithm. This final chapter introduces a novel weighting scheme to counteract non-uniformity in point sets, a feature detection algorithm with mathematical guarantees, and an iterative denoising scheme for point sets.
Popular science and other writings
(↑ top)"Die Deutsche SchülerAkademie" and Interview
2024: Martin Skrodzki
In: Stephanie Schiemann (ed.), Interesse für Mathematik wecken – Talente fördern
The book is devoted to diverse experiences and contacts with regard to mathematical support opportunities for pupils inside and outside the classroom. Numerous people actively involved present a wide range of mathematical offers, support projects and mathematics competitions. Former participants and mathematical luminaries also have their say. They answer the editor's questions about their personal mathematical careers: their support, training and their current field of activity. Pedagogical and psychological aspects frame the experiences. I contributed a chapter describing a specific opportunity format: The "Deutsche SchülerAkademie". Furthermore, I was interviewed on my own (mathematical) CV.
Download the chapter "Die Deutsche SchülerAkademie" Download the interview with me the book
Interview Kevin Walker: An algorithmic approach to mathematical art
2024: Martin Skrodzki, Milena Damrau
In: w/k – Between Science & Art
In this conversation, Milena Damrau and Martin Skrodzki speak with Kevin Walker about the role of mathematics in his artistic practice. Kevin Walker is a Utah-based artist who finds inspiration for his mathematical art in nature.
Space Bending Warehouse Traversal
2023: Ravi Snellenberg and Martin Skrodzki
In: Mathekalender
The calendar offers fascinating insights into recent application-oriented mathematical research and into the everyday professional life of mathematicians. The 24 challenging puzzles are aimed at curious high school students, university students, teachers, and everyone interested.
Exercise and Solution as Download Website of the Mathekalender
Interview Timea Tihanyi: Mathematics and 3D-Printing Ceramic Objects
2023: Martin Skrodzki, Milena Damrau
In: w/k – Between Science & Art
In this conversation, Milena Damrau and Martin Skrodzki speak with Timea Tihanyi about the role of mathematics in her artistic practice. Timea Tihanyi is a Hungarian born interdisciplinary visual artist and ceramist living and working in Seattle, Washington.
Interview Dominic Hopkinson: Building Blocks of Space – Mathematical Sculpting
2023: Martin Skrodzki, Milena Damrau
In: w/k – Between Science & Art
In this conversation, Milena Damrau and Martin Skrodzki speak with Dominic Hopkinson about the role of mathematics in his artistic practice. Dominic Hopkinson generates sculptures in stone, wood, plaster, and bronze, attempting to distill these complex concepts into pure visual form. He lives in the UK.
Introducing Milena Damrau and Martin Skrodzki
2023: Milena Damrau, Martin Skrodzki
In: w/k – Between Science & Art
The core editorial team of w/k strives to win specialists for certain aspects of the major topic Art and Science, which have not yet been sufficiently presented in the online journal. Recently, Milena Damrau and Martin Skrodzki joined the team, whom we warmly welcome. In their article, they explain their motivation to expand the representation of mathematics and arts collaboration in w/k in the future.
A Special Game
2022: Alex McDonough, Ulrich Reitebuch, and Martin Skrodzki
In: Mathekalender
The calendar offers fascinating insights into recent application-oriented mathematical research and into the everyday professional life of mathematicians. The 24 challenging puzzles are aimed at curious high school students, university students, teachers, and everyone interested.
Exercise and Solution as Download Website of the Mathekalender
On the first two “Mathematics and Arts” minisymposia at annual meetings of the German Mathematical Society
2021: Milena Damrau and Martin Skrodzki
In: Art.Salon
At first glance, the areas of mathematics and arts seem very separated and almost impossible to combine within a given project. Yet, history is surprisingly rich in examples for such fruitful interplays and the last decades saw an increase in both conference- and journal formats to further support interdisciplinary interaction between mathematics and arts. A new event along these lines is a minisymposium which provides opportunities for further exchange, networking, and inspiration.
 Image Credit: Teresa Hunyadi.
Image Credit: Teresa Hunyadi.
Mathematik und Kunst – Wie passt das zusammen?
2021: Milena Damrau and Martin Skrodzki
In: Blog der Deutschen Mathematiker-Vereinigung
Auf der DMV Jahrestagung 2020 fand das erste Minisymposium im Schnittbereich Mathematik und Kunst statt. Dieser Artikel berichtet kurz von den Ergebnissen und weiteren Planungen.
Three-dimensional skin-coloring of a four-dimensional being
2020: Martin Skrodzki and Ulrike Bath
In: Art Abstracts of the ALife2020 Conference
Why do tigers and zebras have stripes while other animals like cows or leopards are spotted? This is part of the broader question of morphogenesis. One person to attempt an answer to this question was Alan M. Turing. In this artistic video, we explore a three-dimensional version of his model.
Chip Firing
2020: Martin Skrodzki, Caroline J. Klivans, and Pedro F. Felzenszwalb
In: “Illustrating Mathematics”, Diana Davis (Ed.), AMS
Chip firing is a process on a graph, which is a network of vertices connected by edges. Initially, a stack of “chips” is placed on each vertex. A vertex is allowed to “fire” its chips if it has at least one chip for each vertex to which it is connected (its “neighbors”). When a vertex fires, it sends one chip to each neighbor. We repeat this process until no vertex has enough chips to fire, which we call a “final configuration.”
Der Geschenkequader
2018: Ulrich Reitebuch and Martin Skrodzki
In: Mathekalender
The calendar offers fascinating insights into recent application-oriented mathematical research and into the everyday professional life of mathematicians. The 24 challenging puzzles are aimed at curious high school students, university students, teachers, and everyone interested.
Exercise and Solution as Download Website of the Mathekalender
Sorting presents
2017: Ulrich Reitebuch and Martin Skrodzki
In: Mathekalender
The calendar offers fascinating insights into recent application-oriented mathematical research and into the everyday professional life of mathematicians. The 24 challenging puzzles are aimed at curious high school students, university students, teachers, and everyone interested.
Exercise and Solution as Download Website of the Mathekalender
Wie schnell sortiert man Menschenmassen?
2017: Martin Skrodzki
In: Expuls – Zeitung für den CdE
Sudokus und magische Quadrate sind bekannte Zahlenrätsel. In der Rubrik „Ungelöste Fragen“ geht es um Quadrate, in die nicht eine, sondern gleich zwei Zahlen eingetragen werden. Deren Sortierungen können dann zum Beispiel in Simulationen von Menschenmengen genutzt werden.
Chladni Towers
2017: Martin Skrodzki, Ulrich Reitebuch, and Konrad Polthier
In: ADMC 2017 catalogue
In 1802, Ernst Florens Friedrich Chladni published his book “Acoustics”. The book describes amongst other things an experiment by which different modes of vibration can be visualized. We generalize Chladni's concept to the third dimension. However, we do not build a physical experiment, but simulate the outcome of it, to print it via a 3D-printer. Applications of our method can be found for example in Architecture, where the printed model gives an impression of the acoustics of a given room.